Les vecteurs :

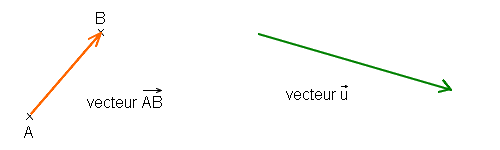
Un vecteur est une flèche. Les vecteurs sont utiles en sciences physiques pour représenter une force, un déplacement, une vitesse. En maths ils servent surtout à créer des repères pour se repérer avec des coordonnées dans un plan ou dans l'espace. Notation: Si un vecteur va d'un point A à un point B on le note AB. Si le point d'origine et d'arrivée n'ont pas de nom, on peut juste noter le vecteur avec une petite flèche au dessus d'une lettre en minuscule, par exemple le vecteur u.

Opérations avec des vecteurs :

Égalité de vecteurs :
On dit que deux vecteurs sont égaux si ils ont la mêmedirection, le mêmesens, et la même longueur. Ils peuvent cependant avoir un point d'origine différent.

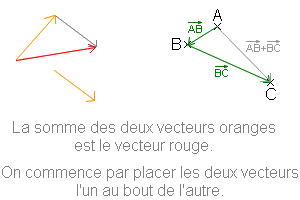
Somme de vecteurs :
La somme de deux vecteurs qui sont placés l'un au bout de l'autre est le vecteur qui part de l'origine du premier et qui arrive à l'extrémité du second. Si A, B et C sont 3 points on a toujours AB+BC=AC (relation de Chasles).

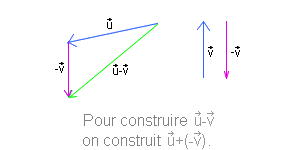
Différence de vecteurs:
La différence de deux vecteurs c'est la somme du premier et de l'opposé du second. L'opposé d'un vecteur u c'est un vecteur de même longueur et de même direction que u mais de sens opposé (la flèche est tournée de l'autre côté). Si A et B sont deux points on a toujours AB=-BA.

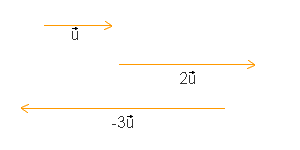
Produit ou quotient d'un vecteur par un nombre :
Le produit (ou lequotient) d'un vecteur u par un nombre k est un vecteur de même direction que u, de longueur multipliée (ou divisée) par k, et de sens contraire à celui de u si k est négatif.

Remarques :

• Si deux vecteurs ont la même direction on dit qu'ils sontcolinéaires.
• Le produit deux vecteurs entre eux existe aussi: c'est leproduit scalaire que nous verrons en première.
• Il n'est pas possible de diviser deux vecteurs entre eux (sauf si ils sont colinéaires), ni d'additionner ou de soustraire des nombres avec des vecteurs.

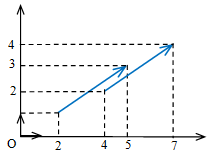
Repérage dans le plan :

Un plan est une surface plate infinie. Les vecteurs permettent de repérer la position de points dans un plan. Pour cela on utilise deux vecteurs non colinéaires que l'on place à une même origine. On obtient un repère du plan.

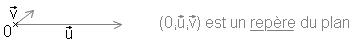
Exemples :
Lorsque les vecteurs u et v forment un angle droit on dit que le repère est orthogonal. Si en plus ils sont tous deux de même longueur on dit que le repère est orthonormé.

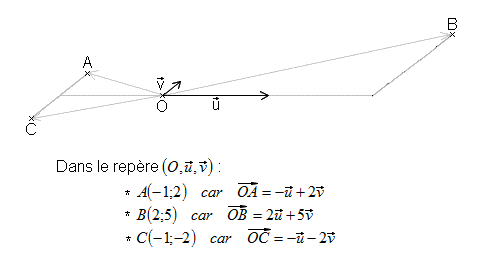
Calculs dans un repère :

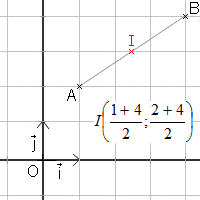
Coordonnées du milieu de deux points :
Si dans un repère on connaît les coordonnées de deux points A(xa;ya) et B(xb;yb) alors on peut calculer les coordonnées du point I(xi;yi) milieu de [AB]. Pour cela on calcule la moyenne des coordonnées de A et de B.

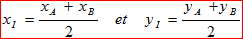
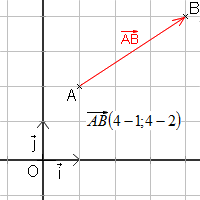
Coordonnées d'un vecteur :
Dans un repère chaque vecteur possède des coordonnées. A chaque vecteur correspond un couple de coordonnées et à chaque couple de coordonnées correspond un vecteur. L'abscisse d'un vecteur c'est de combien il avance et son ordonnée c'est de combien il monte. Si un vecteur passe par deux points A(xa;ya) et B(xb;yb), alors :

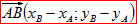
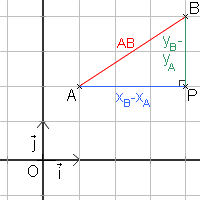
Distance entre deux points :
Dans un repère orthonormé, si A(xa;ya) et B(xb;yb) alors la longueur AB vaut √(〖(xb-xa)〗^2+〖(yb-ya)〗^2 ) . Cette propriété provient du théorème de Pythagore dans le triangle rectangle APB ci-contre. Pour cet exemple on obtient AB=√13.

Colinéarité :
Dans un repère si deux vecteurs u(x;y) et y(x^';y^') sont colinéaires, alors xy’-x’y=0. Réciproquement si dans un repère deux vecteurs u(x;y) et v(x';y') sont tels que xy’-x’y=0 alors ils sont colinéaires. En effet si u(x;y) et v(x';y') sont colinéaires alors on peut trouver un nombre k tel que v=k*u. Donc les coordonnées de v sont égales aux coordonnées de u multipliées par un même nombre k (les coordonnnées de deux vecteurs sont proportionnelles). On a donc:

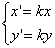
En isolant k dans une équation et en remplaçant sa valeur dans l'autre équation on obtient: